커 블랙홀
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
커 블랙홀은 아인슈타인 장 방정식의 해로, 회전하는 블랙홀을 의미한다. 일반 상대성 이론에서 알려진 네 가지 블랙홀 해 중 하나이며, 커-뉴먼 블랙홀과 함께 회전하는 블랙홀의 유형이다. 커 블랙홀은 질량, 선운동량, 각운동량, 위치 벡터, 전하의 11가지 수로 설명되며, 천체물리학적 블랙홀로 간주된다. 이러한 블랙홀은 항성의 중력 붕괴나 천체의 충돌로 형성될 수 있으며, 펜로즈 과정을 통해 에너지를 생성할 수 있다. 커 블랙홀은 외부 영역에서 커 메트릭과 커-뉴먼 메트릭으로 표현되며, 빛의 굴절과 왜곡을 일으킨다. 2022년에는 커 블랙홀의 평형 상태가 안정적임이 수학적으로 증명되었다. 커 블랙홀은 대중문화, 특히 《Steins;Gate》와 영화 《인터스텔라》에서 중요한 소재로 활용되었다.
더 읽어볼만한 페이지
2. 블랙홀의 종류
일반 상대성이론에서 알려진 정확한 블랙홀 해는 네 가지가 있다. 그중 커 블랙홀과 커-뉴먼 블랙홀은 회전한다. 일반적으로 모든 블랙홀은 안정적인 블랙홀로 빠르게 붕괴한다고 여겨지며, 무모발 정리에 따르면(양자 요동을 제외하고) 안정적인 블랙홀은 다음 11개의 수로 완전히 설명될 수 있다.
- 질량-에너지 등가 원리에 따른 질량-에너지 ''M''
- 선운동량 '''P''' (세 성분)
- 각운동량 '''J''' (세 성분)
- 위치 벡터 '''X''' (세 성분)
- 전하 ''Q''
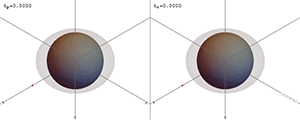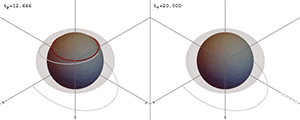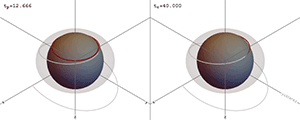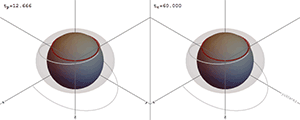

이러한 수치는 전자기장과 중력장을 조사하여 원거리에서 결정할 수 있는 물체의 보존된 속성을 나타낸다. 블랙홀의 다른 모든 변화는 무한대로 빠져나가거나 블랙홀에 빨려 들어간다. 이는 블랙홀 지평선 내부에서 발생하는 어떤 일도 외부 사건에 영향을 미칠 수 없기 때문이다.
블랙홀의 종류는 아래 표와 같이 네 가지로 나눌 수 있다.
천체물리학적 블랙홀은 회전하는 항성체의 붕괴를 통해 형성되기 때문에 0이 아닌 각운동량을 갖지만, 어떤 순 전하도 빠르게 반대 전하를 끌어들여 중화되기 때문에 유효하게 0인 전하를 갖는 것으로 예상된다. 이러한 이유로 "천체물리학적" 블랙홀이라는 용어는 일반적으로 커 블랙홀에 사용된다.[5]
2. 1. 슈바르츠실트 블랙홀
일반 상대성이론에서 알려진 블랙홀 해는 네 가지가 있는데, 그중 회전하지 않는 블랙홀이 슈바르츠실트 블랙홀이다. 블랙홀은 질량-에너지, 선운동량, 각운동량, 위치 벡터, 전하 등 11개의 수로 설명할 수 있다. 이 중 각운동량이 0이고 전하도 0인 경우가 슈바르츠실트 블랙홀이다. 다른 블랙홀로는 회전하는 커 블랙홀, 전하를 가진 라이스너-노르트스트룀 블랙홀, 회전하면서 전하도 가진 커-뉴먼 블랙홀이 있다. 천체물리학적 블랙홀은 회전하는 항성체의 붕괴로 형성되므로 각운동량을 가지지만, 전하는 중화되어 0이 되는 경향이 있다.[5]2. 2. 커 블랙홀
일반 상대성이론에서 알려진 정확한 블랙홀 해는 네 가지가 있으며, 그중 회전하는 블랙홀은 커 블랙홀과 커-뉴먼 블랙홀 두 가지이다. 일반적으로 모든 블랙홀은 안정적인 블랙홀로 빠르게 붕괴하며, 무모발 정리에 따르면 안정적인 블랙홀은 다음 11개의 수로 완전히 설명할 수 있다.- 질량-에너지 등가 원리에 따른 질량-에너지 ''M''
- 선운동량 '''P''' (세 성분)
- 각운동량 '''J''' (세 성분)
- 위치 벡터 '''X''' (세 성분)
- 전하 ''Q''
이 수치들은 전자기장과 중력장을 조사하여 원거리에서 결정할 수 있는 물체의 보존된 속성을 나타낸다. 블랙홀의 다른 모든 변화는 무한대로 빠져나가거나 블랙홀에 빨려 들어간다.
이러한 특성에 따라 네 가지 유형의 블랙홀을 다음과 같이 정의할 수 있다.
천체물리학적 블랙홀은 회전하는 항성체의 붕괴로 형성되기 때문에 0이 아닌 각운동량을 갖지만, 유효 전하는 0인 것으로 예상된다. 따라서 "천체물리학적" 블랙홀은 일반적으로 커 블랙홀을 의미한다.[5]
회전 블랙홀은 아인슈타인 장 방정식의 해이다. 외부 영역에서 모든 회전 블랙홀 해를 대표하는 것으로 여겨지는 두 가지 알려진 정확한 해는 커 메트릭과 커-뉴먼 메트릭이다.
블랙홀 근처에서는 공간이 심하게 휘어져 빛이 굴절되고, 매우 가까운 빛은 여러 번 공전할 수 있다.[11] 2021년에는 커 블랙홀의 적도면 주위에서 빛이 휘어지는 현상에 대한 완전한 수학적 설명이 발표되었다.[12]
2022년, 로이 커가 1963년에 발견한 평형 상태가 안정적이라는 것이 수학적으로 증명되었다.[13]
2. 3. 라이스너-노르트스트룀 블랙홀
2. 4. 커-뉴먼 블랙홀
일반 상대성이론에서 알려진 정확한 블랙홀 해는 네 가지가 있는데, 그중 커 블랙홀과 커-뉴먼 블랙홀은 회전하는 블랙홀이다. 모든 블랙홀은 안정적인 상태로 빠르게 붕괴하며, 무모발 정리에 따르면 안정적인 블랙홀은 다음 11개의 수로 완전히 설명할 수 있다.- 질량-에너지 ''M''
- 선운동량 '''P''' (세 성분)
- 각운동량 '''J''' (세 성분)
- 위치 벡터 '''X''' (세 성분)
- 전하 ''Q''
이러한 수치는 전자기장과 중력장을 통해 원거리에서 결정할 수 있는 보존된 속성을 나타낸다. 블랙홀의 다른 모든 변화는 무한대로 빠져나가거나 블랙홀에 흡수된다. 이는 블랙홀 지평선 내부에서 발생하는 일은 외부에 영향을 줄 수 없기 때문이다.
이러한 특성에 따라 네 가지 유형의 블랙홀을 다음과 같이 정의할 수 있다.
회전 블랙홀은 질량이 큰 회전하는 항성의 중력 붕괴나 총 각운동량이 0이 아닌 다수의 밀집 천체, 항성 또는 가스의 붕괴나 충돌로 형성된다. 알려진 모든 항성은 자전하고 현실적인 충돌은 0이 아닌 각운동량을 가지므로, 자연계의 모든 블랙홀은 회전 블랙홀일 것으로 예상된다.[1][2] 관측된 천체는 상당한 순 전하를 가지고 있지 않으므로, 커 해만이 천체물리학적으로 관련이 있다.
천체물리학적 블랙홀은 회전하는 항성의 붕괴로 형성되므로 각운동량이 0이 아니지만, 순 전하는 빠르게 중화되어 유효 전하는 0이 될 것으로 예상된다. 따라서 "천체물리학적" 블랙홀은 일반적으로 커 블랙홀을 의미한다.[5]
3. 블랙홀의 형성
2006년 말, 천문학자들은 ''천체물리학 저널''에서 블랙홀의 자전 속도 추정치를 보고했다. 우리 은하에 있는 블랙홀 GRS 1915+105는 초당 1,150회 회전할 수 있으며,[6] 이론적 상한선에 근접한다.
> '''블랙홀의 형성''' 섹션의 내용은 커 블랙홀의 일반적인 형성과정을 설명하고 있습니다. 하위 섹션에서는 항성 붕괴, 천체 충돌, 감마선 폭발과의 관계 등 구체적인 형성 메커니즘을 다루고 있으므로, 본문에서는 간략하게 요약된 내용을 제시하고, 자세한 내용은 하위 섹션에서 다루도록 구성하였습니다.
3. 1. 항성 붕괴
회전 블랙홀은 질량이 큰 회전하는 항성의 중력 붕괴 또는 총 각운동량이 0이 아닌 다수의 밀집 천체, 항성 또는 가스의 붕괴나 충돌로 형성된다. 알려진 모든 항성은 자전하고 현실적인 충돌은 0이 아닌 각운동량을 가지므로, 자연계의 모든 블랙홀은 회전 블랙홀일 것으로 예상된다.[1][2] 관측된 천체는 상당한 순 전하를 가지고 있지 않으므로, 커 해만이 천체물리학적으로 관련이 있다.
2006년 말, 천문학자들은 ''천체물리학 저널''에서 블랙홀의 자전 속도 추정치를 보고했다. 우리 은하에 있는 블랙홀 GRS 1915+105는 초당 1,150회 회전할 수 있으며,[6] 이론적 상한선에 근접한다.
3. 2. 천체 충돌
회전 블랙홀은 질량이 큰 회전하는 항성의 중력 붕괴 또는 총 각운동량이 0이 아닌 다수의 밀집 천체, 항성, 가스의 붕괴나 충돌로 형성된다. 알려진 모든 항성은 자전하고 현실적인 충돌은 0이 아닌 각운동량을 가지므로, 자연계의 모든 블랙홀은 회전 블랙홀일 것으로 예상된다.[1][2]
2006년 말, 천문학자들은 ''천체물리학 저널''에서 블랙홀의 자전 속도 추정치를 보고했다. 우리 은하에 있는 블랙홀 GRS 1915+105는 초당 1,150회 회전할 수 있으며,[6] 이론적 상한선에 근접한다.
3. 3. 감마선 폭발과의 관계
회전 블랙홀은 질량이 큰 회전하는 항성의 중력 붕괴나 총 각운동량이 0이 아닌 다수의 밀집 천체, 항성 또는 가스의 붕괴 또는 충돌로 형성된다. 알려진 모든 항성은 자전하고 현실적인 충돌은 0이 아닌 각운동량을 가지므로, 자연계의 모든 블랙홀은 회전 블랙홀일 것으로 예상된다.[1][2]
초신성폭발(하이퍼노바)에 의한 회전하는 블랙홀의 형성은 감마선 폭발의 방출로 관측될 것으로 생각된다.
4. 블랙홀의 특성
일반 상대성이론에서 알려진 정확한 블랙홀 해는 네 가지가 있다. 그중 커 블랙홀과 커-뉴먼 블랙홀 두 가지는 회전한다. 일반적으로 모든 블랙홀은 안정적인 블랙홀로 빠르게 붕괴한다고 여겨지며, 무모발 정리에 따르면(양자 요동을 제외하고) 안정적인 블랙홀은 질량-에너지, 선운동량, 각운동량, 위치 벡터, 전하의 11가지 수치로 설명할 수 있다. 이러한 특성은 원거리에서 전자기장과 중력장을 조사하여 결정할 수 있는 보존된 속성을 나타낸다. 블랙홀의 다른 모든 변화는 무한대로 빠져나가거나 블랙홀에 빨려 들어간다. 이는 블랙홀 지평선 내부에서 발생하는 어떤 일도 외부 사건에 영향을 미칠 수 없기 때문이다.[5]
블랙홀은 그 특성에 따라 다음과 같이 네 가지 유형으로 나눌 수 있다.
천체물리학적 블랙홀은 회전하는 항성체의 붕괴로 형성되기 때문에 각운동량이 0이 아니지만, 순 전하는 빠르게 중화되어 0에 가까워진다. 따라서 "천체물리학적 블랙홀"은 보통 커 블랙홀을 의미한다.[5]
회전하는 블랙홀은 펜로즈 과정을 통해 회전 에너지를 사용하여 많은 에너지를 생성할 수 있다.[7][8] 이 과정은 블랙홀의 사건 지평선 바깥 영역인 에르고스피어 내부에서 발생한다.[9] 에너지 추출 과정을 통해 회전하는 블랙홀은 슈바르츠실트 블랙홀로 감소할 수 있지만, 커 블랙홀의 회전 속도는 절대 0이 되지 않는다.[10]
4. 1. 무모발 정리
일반 상대성이론에서 알려진 정확한 블랙홀 해는 네 가지가 있다. 그중 커 블랙홀과 커-뉴먼 블랙홀 두 가지는 회전한다. 일반적으로 모든 블랙홀은 안정적인 블랙홀로 빠르게 붕괴한다고 여겨지며, 무모발 정리에 따르면(양자 요동을 제외하고) 안정적인 블랙홀은 다음 11개의 수로 완전히 설명할 수 있다.- 질량-에너지 ''M''
- 선운동량 '''P''' (세 성분)
- 각운동량 '''J''' (세 성분)
- 위치 벡터 '''X''' (세 성분)
- 전하 ''Q''
이러한 수치는 전자기장과 중력장을 조사하여 원거리에서 결정할 수 있는 물체의 보존된 속성을 나타낸다. 블랙홀의 다른 모든 변화는 무한대로 빠져나가거나 블랙홀에 빨려 들어간다. 이는 블랙홀 지평선 내부에서 발생하는 어떤 일도 외부 사건에 영향을 미칠 수 없기 때문이다.
이러한 특성 측면에서 네 가지 유형의 블랙홀은 다음과 같이 정의할 수 있다.
천체물리학적 블랙홀은 회전하는 항성체의 붕괴를 통해 형성되기 때문에 0이 아닌 각운동량을 갖지만, 어떤 순 전하도 빠르게 반대 전하를 끌어들여 중화되기 때문에 유효하게 0인 전하를 갖는 것으로 예상된다. 이러한 이유로 "천체물리학적" 블랙홀이라는 용어는 일반적으로 커 블랙홀에 사용된다.[5]
4. 2. 에너지 추출
회전하는 블랙홀은 그 회전 에너지를 희생하여 많은 에너지를 생성할 수 있다.[7][8] 이는 블랙홀의 사건 지평선 바깥 영역인 에르고스피어 내부에서 펜로즈 과정을 통해 발생할 수 있다.[9] 에너지 추출의 일부 경우에서, 회전하는 블랙홀은 점차적으로 더 이상 에너지를 추출할 수 없는 최소 구성인 슈바르츠실트 블랙홀로 감소할 수 있지만, 커 블랙홀의 회전 속도는 절대 0에 도달하지 않는다.[10]5. 커 계량, 커-뉴먼 계량
회전 블랙홀은 아인슈타인 장 방정식의 해이다. 외부 영역에서 모든 회전 블랙홀 해를 대표하는 것으로 여겨지는 두 가지 알려진 정확한 해가 있는데, 그것은 커 메트릭과 커-뉴먼 메트릭이다.
블랙홀 근처에서는 공간이 너무 많이 휘어져서 빛이 굴절되고, 매우 가까운 빛은 블랙홀 주위를 여러 번 공전할 정도로 많이 굴절될 수 있다. 따라서 먼 배경 은하(또는 다른 천체)를 관측할 때, 비록 점점 더 왜곡되더라도 같은 은하의 이미지를 여러 번 볼 수 있다.[11] 커 블랙홀의 적도면 주위를 빛이 어떻게 휘어지는지에 대한 완전한 수학적 설명은 2021년에 발표되었다.[12]
2022년, 1963년 로이 커가 발견한 평형 상태가 안정적이라는 것이 수학적으로 증명되었고, 따라서 1915년 아인슈타인 방정식의 해였던 블랙홀은 안정적이었다.[13]
5. 1. 커 계량
회전 블랙홀은 아인슈타인 장 방정식의 해이다. 외부 영역에서 모든 회전 블랙홀 해를 대표하는 것으로 여겨지는 두 가지 알려진 정확한 해가 있는데, 그것은 커 메트릭과 커-뉴먼 메트릭이다.[11]
5. 2. 커-뉴먼 계량
회전 블랙홀은 아인슈타인 장 방정식의 해이다. 외부 영역에서 모든 회전 블랙홀 해를 대표하는 것으로 여겨지는 두 가지 알려진 정확한 해가 있는데, 그것은 커 메트릭과 커-뉴먼 메트릭이다.6. 상태 전이
7. 대중문화에서의 블랙홀
커 블랙홀은 2009년 비주얼 노벨 《Steins;Gate》(TV 애니메이션 Steins;Gate, 만화 Steins;Gate도 포함)에서 시간 여행의 가능성 때문에 광범위하게 등장한다.[15] 하지만 이는 이야기를 위해 크게 과장된 것이다.
커 블랙홀은 조 데이비스의 "백조의 노래" 프로젝트의 핵심이기도 하다.[16][17] 또한 2014년 영화 《인터스텔라》의 핵심 요소이기도 하다.
참조
[1]
웹사이트
Why and how do planets rotate?
https://www.scientif[...]
Scientific American
2003-04-14
[2]
웹사이트
This Is Why Black Holes Must Spin At Almost The Speed Of Light
https://www.forbes.c[...]
2019-08-01
[3]
웹사이트
It is said that most black holes likely have spin. What exactly is it that spins?
https://astronomy.co[...]
2019-07-22
[4]
arXiv
The Kerr spacetime: A brief introduction
2008-01-15
[5]
서적
Formation of the First Black Holes
[6]
웹사이트
Black hole spins at the limit
http://www.cosmosmag[...]
2006-11-24
[7]
논문
Amplification of waves from a rotating body
[8]
웹사이트
After 50 Years, Experiment Finally Shows Energy Could Be Extracted From a Black Hole
https://www.sciencea[...]
2020-06-25
[9]
논문
Extracting X rays, Ύ rays, and relativistic e−e+ pairs from supermassive Kerr black holes using the Penrose mechanism
1995
[10]
논문
Energy Extraction from a Rotating Black Hole by Magnetic Reconnection in the Ergosphere
https://dx.doi.org/1[...]
2008-08
[11]
웹사이트
Danish Student solves how the Universe is reflected near black holes
https://nbi.ku.dk/en[...]
2021-08-09
[12]
논문
Divergent reflections around the photon sphere of a black hole
2021-07-09
[13]
Monograph
A Researcher Shores Up Einstein's Theory With Math
https://news.columbi[...]
Columbia University
2022-10-19
[14]
논문
Thermodynamic phase transitions of Kerr-Newman black holes in de Sitter space
[15]
웹사이트
想定科学『Steins;Gate(シュタインズゲート)』公式Webサイト
http://steinsgate.jp[...]
2020-04-29
[16]
웹사이트
Meet the man trying to send a warning about history's worst tragedies back to 1935
https://www.mic.com/[...]
2020-07-23
[17]
Youtube
Летняя школа космического искусства. Summer School of Space Art with Joe Davis
https://www.youtube.[...]
2020-08-10
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
